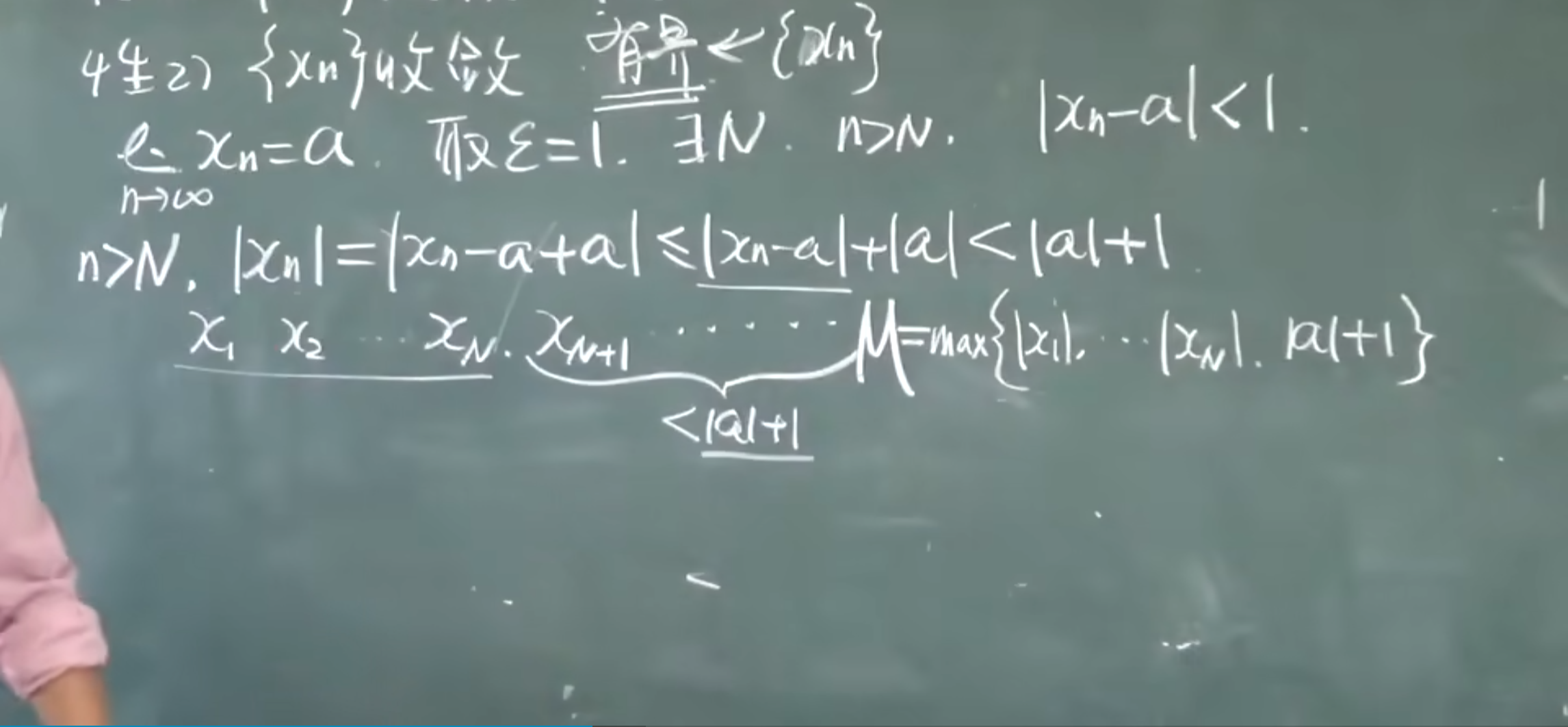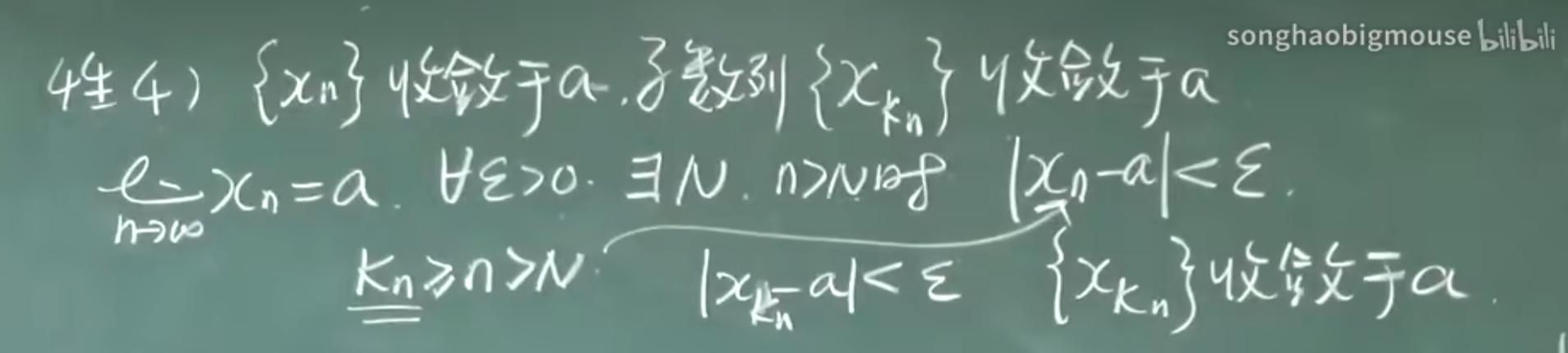文章

数学学习

发表于
作者 nooblong 16 分钟阅读

一、微积分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

1.	函数与极限
•	函数的概念与性质
•	极限与连续
2.	一元微分学
•	导数与微分
•	导数的应用（如单调性、极值、凹凸性等）
•	洛必达法则
•	泰勒公式
3.	一元积分学
•	不定积分
•	定积分
•	积分的应用（如面积、体积、弧长等）
•	反常积分
4.	多元微积分
•	多元函数与偏导数
•	重积分
•	曲线积分与曲面积分
•	格林公式、高斯公式与斯托克斯公式

数列极限

定义:

对于一个实数数列{a_n}，如果存在一个实数 L，对于任意给定的正实数 ε（无论多么小），总存在正整数 N，使得当 n > N 时，就有a_n - L< ε 成立，那么我们称数列 {a_n} 的极限为 L，记作 lim(a_n) = L 或者 a_n → L。

换句话说，数列的极限 L 是指当数列的项足够靠近 L 时，这个数列的后续项都会无限地靠近 L。ε 实际上是一个很小的范围，当数列的值在以 L 为中心、ε 为半径的范围内时，就可以认为这些值都接近 L。

image-20240301173330890

例1

image-20240302202228463

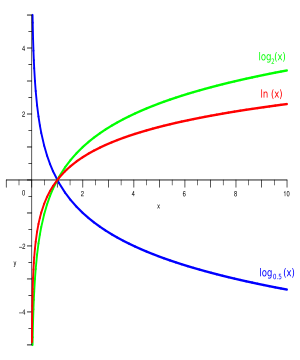
等式两边求对数后等式成立吗？

当对等式两边同时取对数时，等式是否成立取决于所取的对数函数。如果取自然对数（以e为底的对数，通常表示为ln），那么等式仍然成立；如果取常用对数（以10为底的对数，通常表示为log），也可以成立。

当 |q| < 1 时，log q 的值为负数。

img

例2

image-20240302210343369

不等式两边同时取x次方，仍然成立吗

  1. 如果 ( x ) 是一个正实数，并且不等式两边的所有数都是正实数，那么不等式仍然成立。这是因为正实数的幂运算不改变不等式的方向。
  2. 如果 ( x ) 是一个负实数或者是一个小数，并且不等式中包含负数或小数，那么不等式的方向可能会发生变化。取决于 ( x ) 的具体值以及不等式中的数值大小关系。
  3. 在某些特殊情况下，不等式的方向可能会保持不变，但这取决于具体的不等式形式和 ( x ) 的取值范围。

例3

image-20240302211542944

性质：

  1. {Xn}收敛，极限唯一

image-20240303224949229

  1. {Xn}收敛，有界
    1. 有界是收敛的必要条件，不是充分条件
    2. 单调有界，则有极限

image-20240303225712603

  1. limXn n->∞ a>0(a<0) 存在N，n>N时Xn>0

  2. {Xn}收敛于a，子数列{X(Kn)}收敛于a

    证明

    image-20240305235459208

    1. 推论
      1. 找到一个子数列不收敛，则原数列发散
      2. 找到两个子数列，虽然都收敛，但是极限不同，原数列发散
      3. 原数列收敛的 充分必要条件是 奇数列和偶数列构成的子数列收敛，且极限相同
      4. 找到一个子数列收敛，原数列不一定收敛

函数极限

定义:

image-20240308094853308

常用的倒数

img

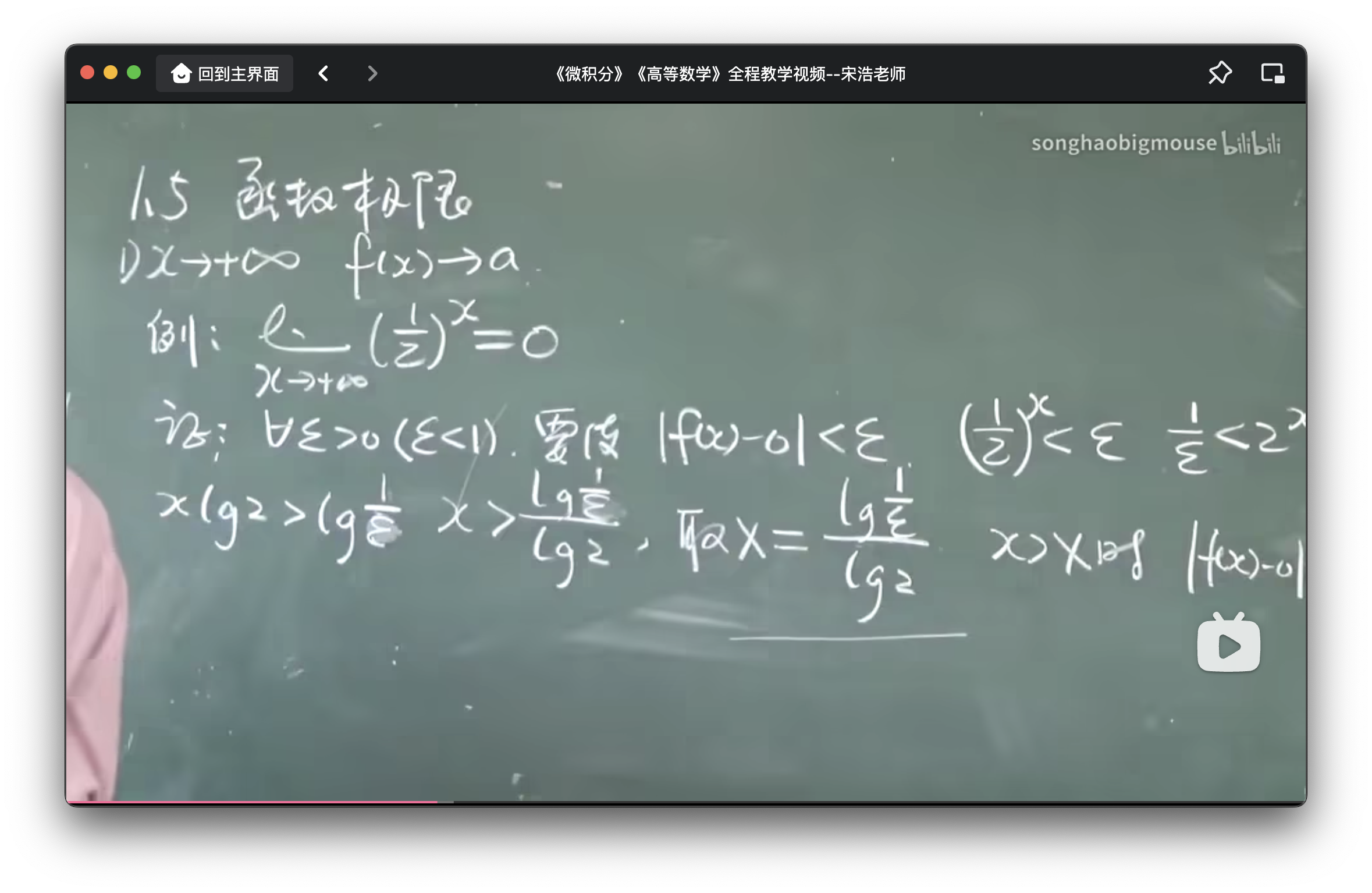
要化简不等式 $( \frac{1}{2^x} < a )$，可以按照以下步骤进行：

  1. 首先，将底数改写为指数形式，得到 $( 2^{-x} < a )$。
  2. 接着，将不等式两边取倒数，并注意改变不等号的方向，得到$ ( \frac{1}{2^{-x}} > \frac{1}{a} )$。
  3. 然后，根据指数的倒数规则，将$ ( 2^{-x} ) $改写为$ ( 2^x )，得到 ( 2^x > \frac{1}{a} )$。
  4. $当以 (e) 为底时，(2) 的 (x) 次方取自然对数的结果为 (\ln(2^x))。根据对数的性质，(\ln(2^x) = x \cdot \ln(2))$

例1：$lim(1/2){^x}=0$

image-20240308103350468

$\forall x \exist x$

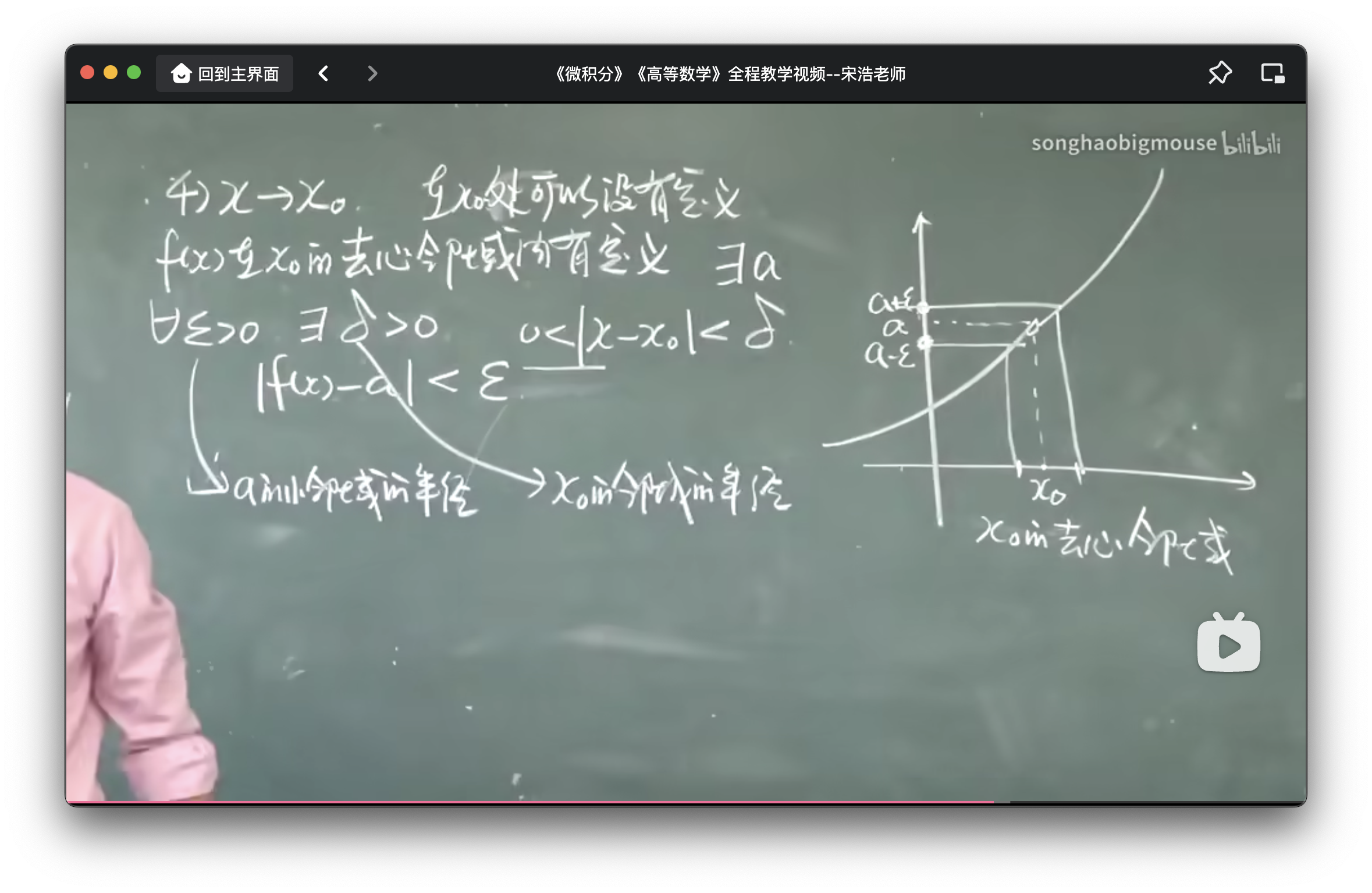
定义2：x->x0

image-20240308115558312

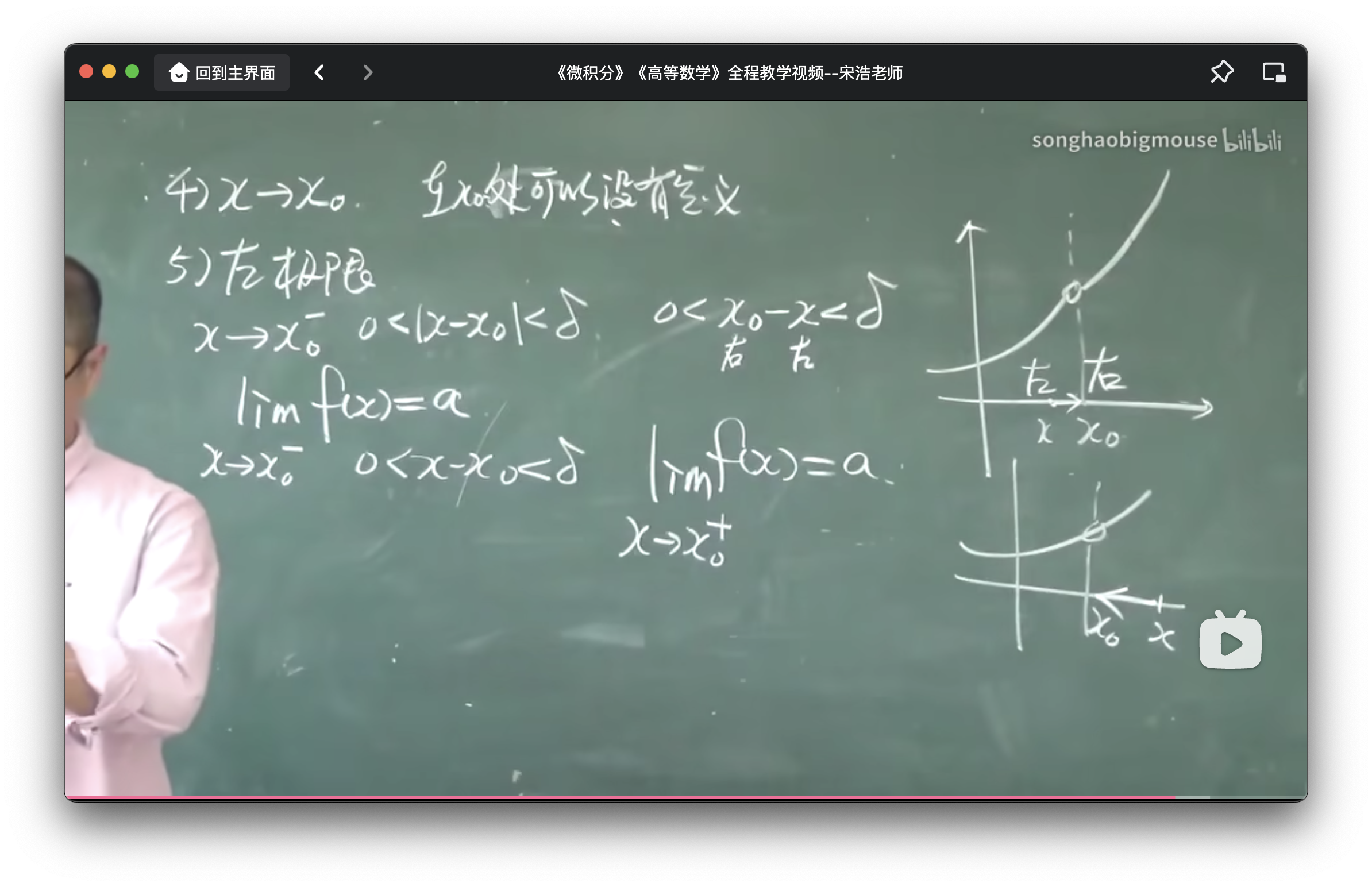
定义3：左极限右极限

image-20240308150123066

性质：

  1. lim f(x)存在，是唯一的
  2. 局部有界性：lim f(x)存在，存在x0的去心邻域
  3. 局部保号性：lim f(x) = a，a>0，在去心邻域里f(x)>0
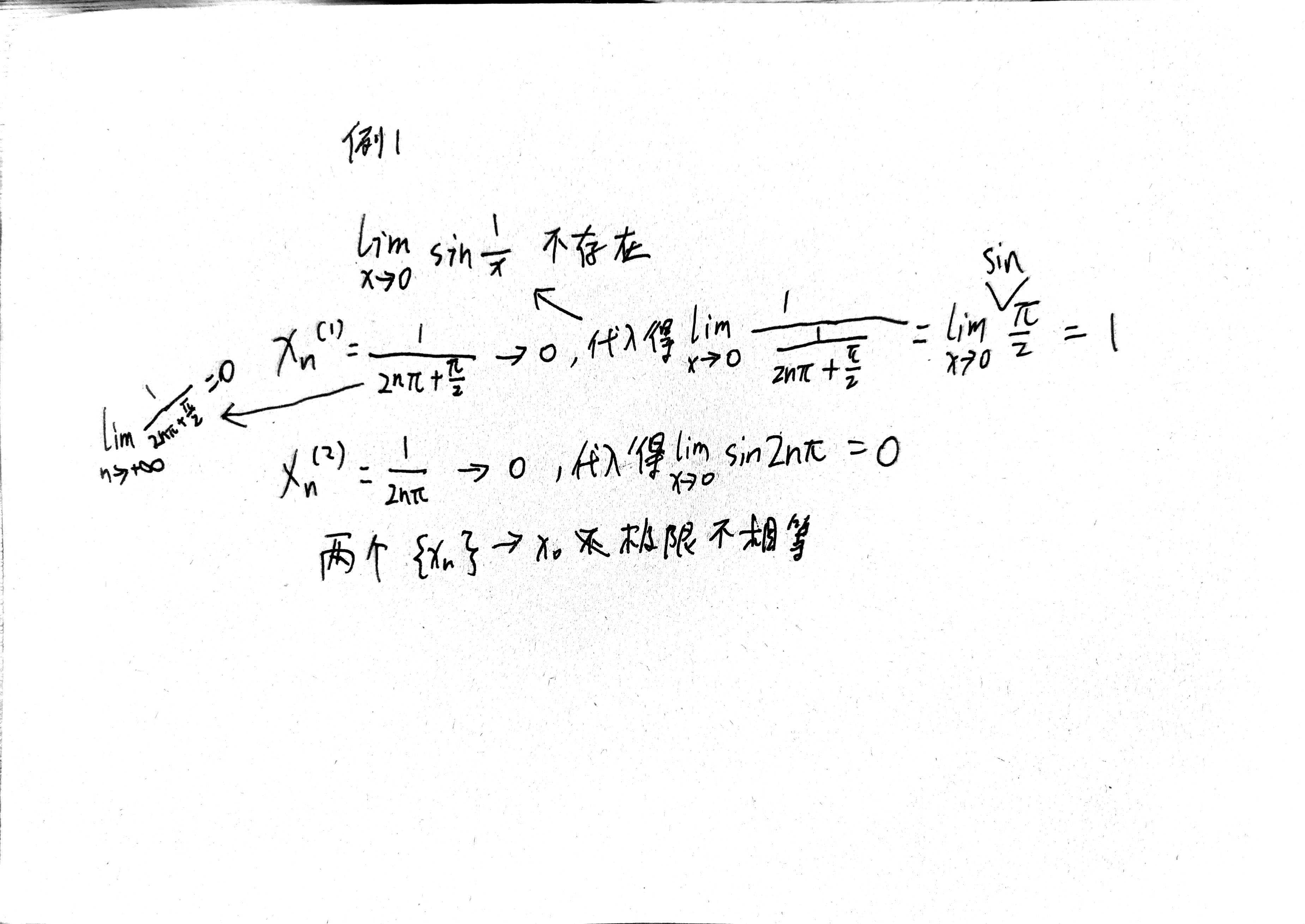
  4. lim f(x)=a (x->x0) 充要条件 当x->x0时，取任意数列{Xn}，当lim Xn (n->+∞) 以X0为极限的时候，代进去lim f(Xn) (n->+∞) = a

例1

image-20240308165330223

无穷小与无穷大

例1：lim x->0 x sin(1/x) = 0

sin(1/x)有界，有界乘以趋于0的就是0

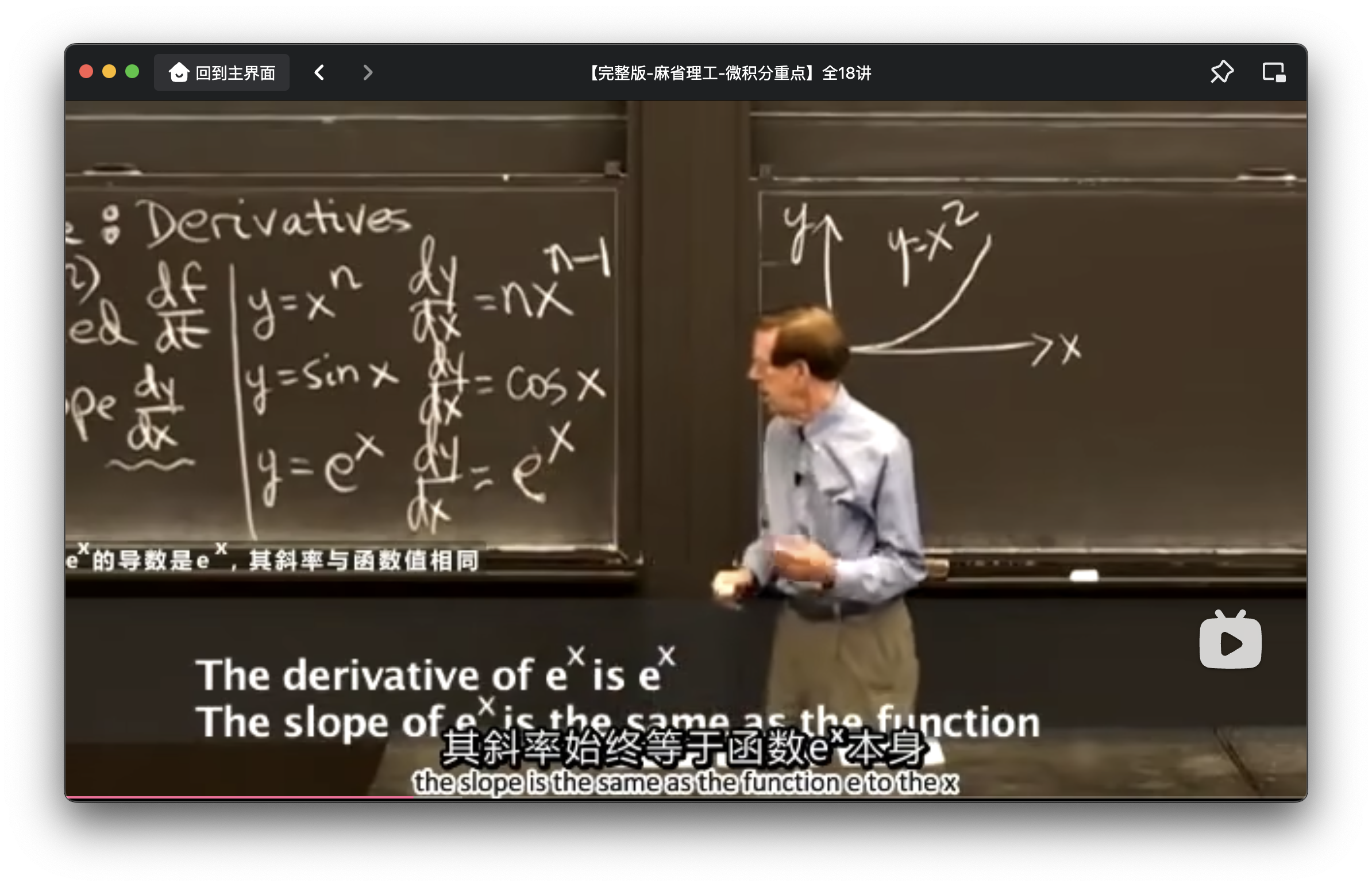
image-20240311105011663

链式法则

image-20240311165608893

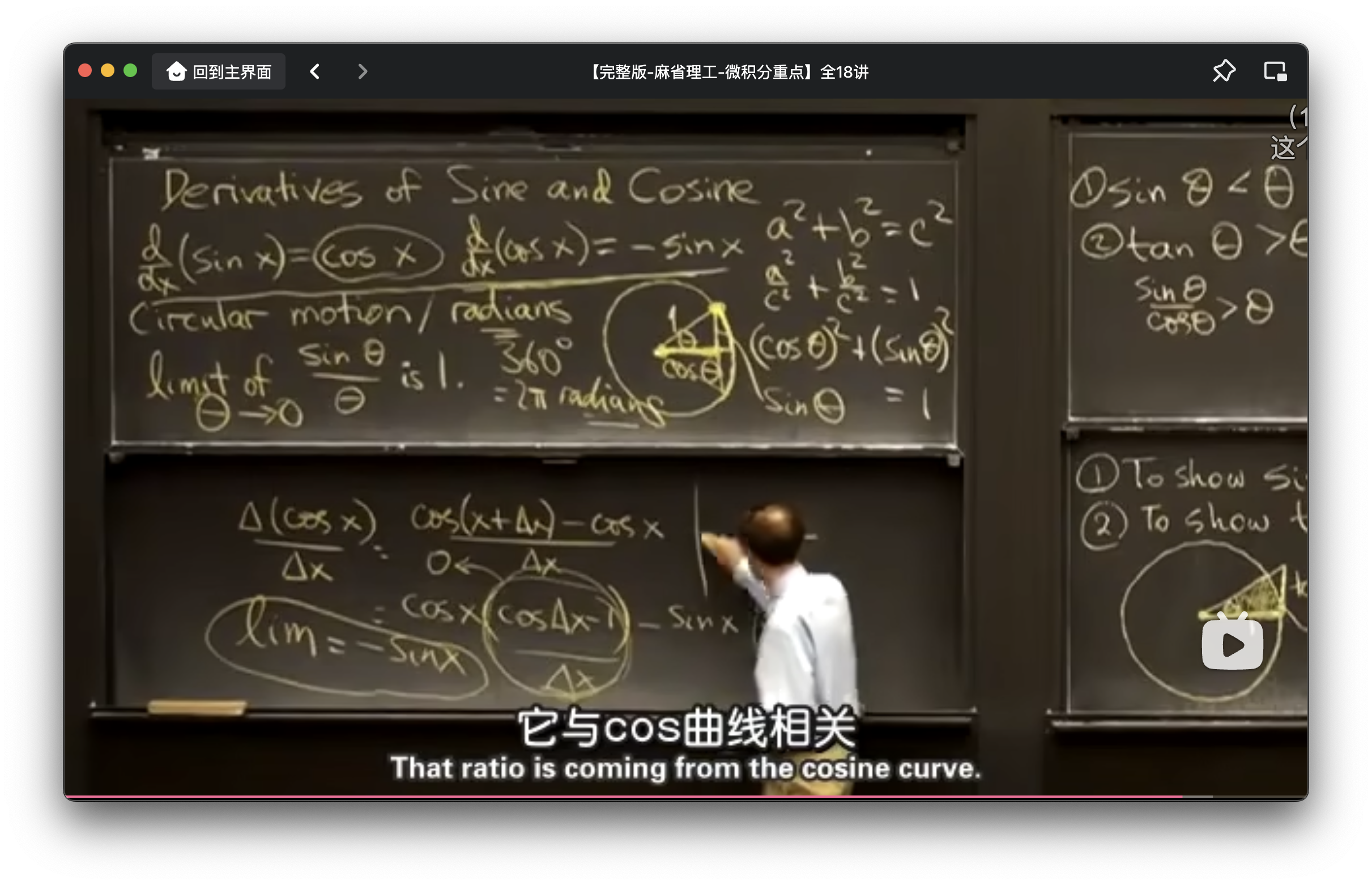
sin(x)’=cos(x)

image-20240312182127532

image-20240312182050232

单变量微积分

$\frac{d}{dx} (\ln u(x)) = \frac{u{\prime}(x)}{u(x)}$

(ln x)’ = 1/x

$v = x^x$ 导数

ln v = x ln x ;

(ln v)’ = ln x + x * 1/x

v’/v = 1 + ln x

v’ = v (1 + ln x)将v=x^x代入

$dx^x/dx = x^x (1 + ln x)$

$\lim_{n \to \infty} (1 + \frac{1}{n})^n$ 为什么 = e

ln 答案 = $ln(1 + 1/n)^n = n*ln(1+1/n)$

设$\Delta x$ = 1/n -> 0

= $1/\Delta x$ $ ln(1+\Delta x)$

= $1/\Delta x$ $ln(1+\Delta x) - ln 1$

可以看做d lnx / dxx = 1
因为ln x’ = 1/x，所以d lnx / dxx = 1结果为1

ln 答案 = $ln(\lim_{n \to \infty} (1 + \frac{1}{n})^n)$ = 1

答案 = $\lim_{n \to \infty} (1 + \frac{1}{n})^n = e^{ln(\lim_{n \to \infty} (1 + \frac{1}{n})^n)}$ = e

使用线性近似

$ln(a_k) = ln(1 + 1/k)^k = k*ln(1+1/k)$

因为ln(1+x) ~= x

ln(a_k) = k*(1/k) = 1,

证明$\frac{dx^r}{dx}=rx^{r-1}$

  1. $x^r = (e^{lnx})^r = e^{rlnx} = e^{rlnx} * (rlnx)’$
  2. $u=x^r$，$\frac{u’}{u} = (lnu)’=\frac r x$，$u’=x^r\frac r x$

$f(x) \approx f(x_0) + f’(x_0)*(x - x_0)$

$\frac{\Delta f} {\Delta x} \approx f’(x_0)$ ($\Delta x = x - x_0$) 当x=x0时，和上面公式一样

ln 1.1 = ?

x0 在 0 时，ln(1+x) ~= f(0) + f’(0)f(x-x0) ~= ln(1) + 1/1+0 * (x - 0) ~= x

x0 在 0 时，(1+x)^r ~= 1 + r(1+0)^r-1 * (x - 0) ~= 1 + rx

ln(1.1)，0.1 ~= 0，~= ln(1 + 1/10)，由上x=1/10，ln(1.1) ~= 1/10

常用：sinx ~= x, cosx ~= 1, e^x ~= 1 + x（x ~= 0）

$\frac {e^{-3x}} {\sqrt {1+x}}$ = e^-3x * (1+x)^1/2 ~= (1-3x) (1 - 1/2x), drop x^2 and higher

$f(x) \approx f(x_0) + f’(x_0)*(x - x_0) + \frac {f’‘(x_0)} 2 (x-x_0)^2$

why 1/2 f’‘(x0)?

f(x) = a + bx + cx^2, f(0) = a

f’(x) = b + 2cx, f’(0) = b

f’‘(x) = 2c, 1/2 f’‘(0) = c

image-20240717095836968

已知加水速率dV/dt = 2

r/h = 4/10, V = 1/3 πr^2h

what is dh/dt when h = 5?

r = 2/5h, V = 1/3 π (2/5h)^2 h

2 = dV/dt = π/3 (2/5)^2 3h^2 dh/dt

dh/dt = 1/2π (升/秒)

牛顿迭代法

$x_{n+1} = x_n - \frac {f(x_n)} {f’(x_n)}$

image-20240718104939526

slove x^2 = 5

从x0 = 2开始，f(x) = x^2 - 5, f’(x) = 2x

$x_1 = x_0 - \frac {x_0^2 - 5} { 2x0} = x_0 - 1/2x_0 + 5/2x_0$

x1 = 1/2 * 2 + 5/4 = 9/4

x2 = 1/2 * 9/4 + 5/2 * 4/9 = 161/72

x3 = 1/2 * 161/72 + 5/2 * 161/72

相同写法

slove (64.1)^(1/3) ~= ?

y = x^1/3, dy = 1/3^(-2/3) dx（dy，dx视作无限小，只是题目取1/10）

A + x = 64, y = 64^(1/3) = 4

dy = 1/3(64)^(-2/3) dx = 1/3 * 1/16 dx = 1/48 dx （线性近似结果）

dx = 1/10, dy = 1/48 dx = 1/480

64.1^(1/3) ~= y + dy = 4 + 1/480

换元法：$\int x^3(x^4+2)^5dx$

u = x^4 + 2, du = 4x^3 dx

= $\int \frac {u^5du} {4} = \frac {1} {24} u^6 + C = \frac {1} {24} (x^4 + 2)^6 + C$

中值定理

费马定理

f在极值点x0 ∈ (a, b)处可导 => f’(x0) = 0

罗尔中值定理

f在[a, b]连续，(a, b)可导

f(a) = f(b) => $\exist \zeta \in $(a,b), f’($\zeta$) = 0

拉格朗日中值定理

f在[a, b]连续，(a, b)可导

=> $\exist \zeta \in (a, b), s.t. f’(\zeta) = \frac {f(b) - f(a)} {b - a}$

科西中值定理

f，g在[a, b]连续，(a, b)可导，g’(x) != 0, $\forall x \in (a,b)$

=> $\exist \zeta \in (a,b), s.t. \frac {f(b) - f(a)} {g(b) - g(a)} = \frac {f’(\zeta)} {g’(\zeta)}$

$G(x) = \int g(x)dx $

积分的唯一性

if F’ = G’, F(x) = G(x) + c

二、线性代数

1
2
3

1.	行列式
•	行列式的定义与性质
2.	矩阵

题目要求

已知：

$ A \vec{v} = \lambda \vec{v} $

矩阵 $ A = \begin{bmatrix} 0 & 1 \ 1 & -1 \end{bmatrix} $。

求 $ A $ 的特征向量和特征值，并计算 $ A^n $ 的表达式。

解答

1. 特征值

特征值满足 $ \det(A - \lambda I) = 0 $。

\[A - \lambda I = \begin{bmatrix} 0 & 1 \\ 1 & -1 \end{bmatrix} - \begin{bmatrix} \lambda & 0 \\ 0 & \lambda \end{bmatrix} = \begin{bmatrix} -\lambda & 1 \\ 1 & -1 - \lambda \end{bmatrix}\]

求行列式：

\[\det(A - \lambda I) = \lambda^2 - \lambda - 1 = 0\]

解得特征值：

\[\lambda = \frac{1 \pm \sqrt{5}}{2}\]

记为：

\[\lambda_1 = \frac{1 + \sqrt{5}}{2}, \quad \lambda_2 = \frac{1 - \sqrt{5}}{2}\]

2. 特征向量

对于特征值 $ \lambda_1 = \frac{1 + \sqrt{5}}{2} $：

\[A - \lambda_1 I = \begin{bmatrix} -\frac{1 + \sqrt{5}}{2} & 1 \\ 1 & -\frac{1 + \sqrt{5}}{2} \end{bmatrix}\]

求解 $ (A - \lambda_1 I) \vec{v} = 0 $，即：

\[-\frac{1 + \sqrt{5}}{2} x + y = 0\]

令 $ x = 1 $，则 $ y = \frac{1 + \sqrt{5}}{2} $。

故特征向量为：

\[\vec{v_1} = \begin{bmatrix} 1 \\ \frac{1 + \sqrt{5}}{2} \end{bmatrix}\]

对于特征值 $ \lambda_2 = \frac{1 - \sqrt{5}}{2} $：

\[A - \lambda_2 I = \begin{bmatrix} -\frac{1 - \sqrt{5}}{2} & 1 \\ 1 & -\frac{1 - \sqrt{5}}{2} \end{bmatrix}\]

求解 $ (A - \lambda_2 I) \vec{v} = 0 $，即：

\[-\frac{1 - \sqrt{5}}{2} x + y = 0\]

令 $ x = 1 $，则 $ y = \frac{1 - \sqrt{5}}{2} $。

故特征向量为：

\[\vec{v_2} = \begin{bmatrix} 1 \\ \frac{1 - \sqrt{5}}{2} \end{bmatrix}\]

3. 求 $ A^n $ 的表达式

设 $ A = P D P^{-1} $，则 $ A^n = P D^n P^{-1} $。

已知：

\[D = \begin{bmatrix} \frac{1 + \sqrt{5}}{2} & 0 \\ 0 & \frac{1 - \sqrt{5}}{2} \end{bmatrix}\] \[D^n = \begin{bmatrix} \left( \frac{1 + \sqrt{5}}{2} \right)^n & 0 \\ 0 & \left( \frac{1 - \sqrt{5}}{2} \right)^n \end{bmatrix}\]

求 $ P $ 和 $ P^{-1} $：

\[P = \begin{bmatrix} 1 & 1 \\ \frac{1 + \sqrt{5}}{2} & \frac{1 - \sqrt{5}}{2} \end{bmatrix}\] \[P^{-1} = \frac{1}{\sqrt{5}} \begin{bmatrix} \frac{\sqrt{5} - 1}{2} & -1 \\ -\frac{\sqrt{5} + 1}{2} & 1 \end{bmatrix}\]

因此，

\[A^n = P D^n P^{-1}\]
1
2
3
4
5
6
7
8
9
10
11
12

•	矩阵的基本运算
•	逆矩阵
•	矩阵的秩
3.	向量空间
•	向量的线性组合与线性相关性
•	基与维数
4.	线性变换
•	线性变换与矩阵的关系
5.	特征值与特征向量
•	特征值的定义与性质
•	矩阵的对角化
6.	二次型

三、常微分方程

1
2
3
4
5
6
7
8
9
10

1.	一阶微分方程
•	分离变量法
•	齐次方程与非齐次方程
•	一阶线性微分方程
2.	高阶微分方程
•	常系数齐次线性微分方程
•	常系数非齐次线性微分方程
•	拉普拉斯变换
3.	微分方程的应用
•	物理、工程中的微分方程模型

四、无穷级数

1
2
3
4
5
6
7
8

1.	数项级数
•	收敛与发散
•	收敛判别法
2.	幂级数
•	幂级数的收敛半径与收敛区间
•	泰勒级数
3.	傅里叶级数
•	傅里叶级数的基本理论

五、向量分析

1
2
3
4
5
6

1.	向量代数与解析几何
•	向量的运算
•	空间解析几何
2.	向量函数
•	向量函数的极限与连续性
•	向量函数的导数与积分

六、复变函数

1
2
3
4
5
6
7
8
9
10
11
12

1.	复数与复平面
•	复数的基本运算
•	复平面与复数的几何意义
2.	解析函数
•	解析函数的定义与性质
•	柯西-黎曼方程
3.	复积分
•	复积分的基本概念
•	柯西积分定理与积分公式
4.	级数展开
•	复变函数的幂级数展开
•	势级数与留数定理

七、概率与统计

1
2
3
4
5
6
7
8

1.	概率论基础
•	概率的基本概念
•	随机变量与分布
•	数学期望与方差
2.	数理统计
•	抽样分布
•	参数估计
•	假设检验

八、数值分析

1
2
3
4
5
6

1.	插值法
•	拉格朗日插值
•	牛顿插值
2.	数值积分与数值微分
3.	线性方程组的数值解法
4.	常微分方程的数值解法
全部, 数学
本文由作者按照 CC BY 4.0 进行授权